Piecewise functions are essential for modeling real-world scenarios with varying rules across different intervals. They help represent complex behaviors succinctly, making them vital in calculus and practical applications. Worksheets with answers provide structured practice, ensuring mastery in graphing, identifying discontinuities, and interpreting piecewise expressions accurately.
Definition and Importance
A piecewise function is a mathematical function defined by multiple sub-functions, each applying to a specific interval of the domain. It is crucial for modeling real-world phenomena with varying rules across different intervals. Understanding piecewise functions is fundamental in calculus and practical applications, as they allow for precise representations of complex behaviors and discontinuities.
Common Examples in Real-World Applications
Piecewise functions are widely used in real-world applications, such as calculating overtime pay, determining cost functions in manufacturing, and modeling temperature changes over time. They provide a flexible framework for representing scenarios where different rules apply under varying conditions, making them indispensable in fields like economics, physics, and engineering.

Graphing Basics
Graphing piecewise functions involves identifying intervals, using open/closed circles, and plotting points. Worksheets provide structured practice, helping students master these essential skills effectively.
Identifying Intervals and Endpoints
Identifying intervals and endpoints is crucial for graphing piecewise functions. Worksheets guide students in pinpointing where each piece applies, ensuring accurate transitions and endpoint representation. Open and closed circles denote inclusivity, while endpoints define function behavior changes. Practice exercises enhance understanding and precision in mapping these critical points effectively for clear function visualization.
Using Open and Closed Circles
Open and closed circles are essential for accurately graphing piecewise functions. Open circles indicate points where the function is not defined or not included, while closed circles mark endpoints that are part of the function. Worksheets with answers emphasize correct placement, ensuring clarity and precision in visual representations of function behavior at interval boundaries.
Plotting Discontinuous Points
Discontinuous points in piecewise functions occur where the function’s left-hand and right-hand limits differ or where the function is undefined. To plot these, use open circles for points excluded from the domain and closed circles for included endpoints. Worksheets with answers guide students in accurately identifying and marking these points for clear graph interpretation.
Points of Discontinuity
Points of discontinuity occur where a piecewise function has abrupt breaks or jumps. These points are crucial for accurate graphing and often involve open or closed circles to denote exclusion or inclusion of specific values, as detailed in worksheets with answers for practice and clarity.
Removable Discontinuities
Removable discontinuities occur when a function has a “hole” at a specific point, often due to a single-point gap. These are addressed by redefining the function at that point. Worksheets with answers highlight such cases, ensuring students can identify and correct them, fostering a clear understanding of function behavior and graphing accuracy.
Jump Discontinuities
Jump discontinuities happen when a function “jumps” between two values at a point, creating a break in the graph. Worksheets with answers guide students in identifying these breaks and accurately plotting the function, emphasizing the importance of open and closed circles to denote the behavior around the discontinuity effectively.
Infinite Discontinuities
Infinite discontinuities occur where a function approaches infinity or negative infinity, creating vertical asymptotes. These are identified by unbounded behavior in the function’s graph. Worksheets with answers guide students in plotting these points, emphasizing the use of open circles and asymptotic lines to represent the function’s behavior accurately near these discontinuities.
Tables of Values for Piecewise Functions
Tables of values help visualize piecewise functions by listing x and corresponding f(x) values. This method simplifies plotting points, especially for different intervals. Worksheets with answers provide clear examples, aiding in understanding how expressions change across domains, and ensure accurate graphing.
Creating a Table for Different Domains
Creating a table for different domains involves listing x-values and corresponding f(x) values. This method organizes data, making it easier to identify patterns and transitions between function pieces. Worksheets often include blank tables for students to fill, ensuring understanding of how functions behave across distinct intervals.
Calculating f(x) for Given x Values
Calculating f(x) for given x-values in piecewise functions involves determining the appropriate function piece based on the x-value’s interval. For each x, identify the corresponding function piece, apply its formula, and compute the result. Pay attention to interval definitions to ensure correct calculations at boundary points and handle discontinuities as defined.
Interpreting the Table for Graphing
Interpreting a table for graphing involves matching x-values to their corresponding f(x) values. Plot each point accurately on the graph, using open or closed circles based on the function’s definition at endpoints. This process ensures the correct visual representation of the piecewise function, aiding in identifying intervals, discontinuities, and overall behavior.
Answer Key and Solutions
The answer key provides correct solutions for graphing piecewise functions, helping verify accuracy. It highlights common errors, ensuring understanding and improving problem-solving skills effectively through clear explanations.
How to Use Answer Keys Effectively
To use answer keys effectively, start by attempting problems independently. Compare your solutions with the provided answers to identify errors. Focus on understanding the reasoning behind correct answers, and review common mistakes. This method enhances learning and improves graphing accuracy for piecewise functions through structured practice and feedback.
Common Mistakes in Solutions
Common errors include misidentifying domain intervals, using incorrect open or closed circles, and neglecting points of discontinuity. Students often mix up function pieces or mislabel endpoints, leading to inaccurate graphs. Carefully checking each interval and endpoint helps minimize these mistakes and ensures precise solutions when graphing piecewise functions.
Verifying Answers for Accuracy
Verify solutions by checking each step, ensuring function pieces align with domains and graphs match expected behavior. Compare with answer keys to confirm correctness. Pay attention to points of discontinuity and proper use of open/closed circles. Understanding errors helps refine accuracy and mastery in graphing piecewise functions effectively.
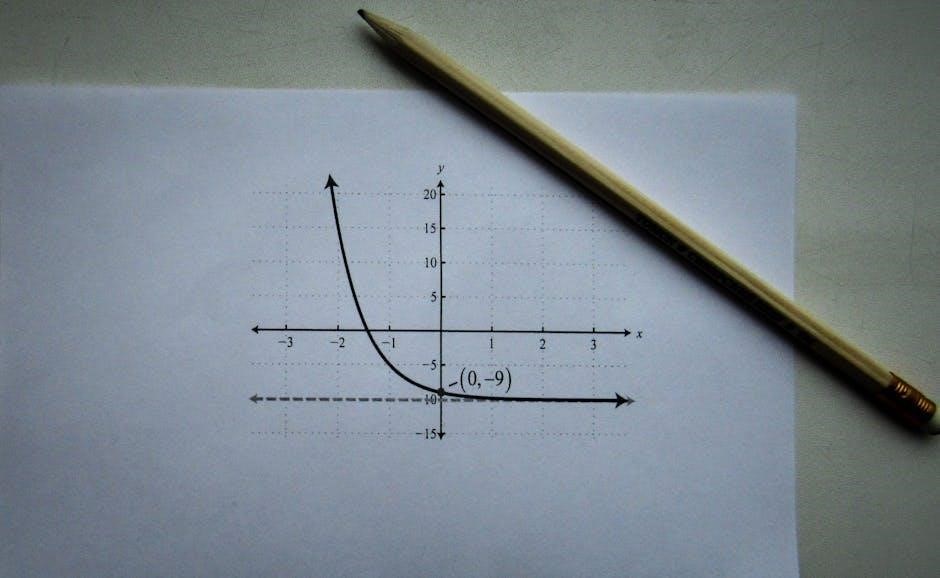
Writing Piecewise Functions
Writing piecewise functions involves defining intervals and assigning corresponding expressions. Ensure each piece aligns with its domain and verify continuity at interval endpoints for accuracy and correctness.
From Graph to Function
Converting graphs to piecewise functions involves identifying intervals and corresponding expressions. Analyze the graph’s behavior, noting changes at breakpoints. Assign expressions based on observed trends, ensuring continuity or defined discontinuities; Verify by plotting the function to match the original graph accurately, confirming each piece aligns with its domain. Practice with worksheets enhances this skill.
Defining Pieces Based on Domain Intervals
Identify the domain intervals where the function behaves differently. For each interval, determine the specific expression that defines the function within that range. Ensure each piece is correctly assigned to its interval, maintaining continuity or addressing discontinuities as needed. Worksheets with answers provide clear examples to master this process effectively.
Ensuring Continuity and Correctness
Verify that each piece of the function connects correctly at interval endpoints to maintain continuity. Check for any discontinuities and classify them as removable, jump, or infinite. Use worksheets with answers to practice identifying and resolving errors, ensuring the function is graphed accurately and adheres to mathematical principles.

Real-World Applications
Piecewise functions model real-world scenarios like overtime pay, cost manufacturing, and temperature changes. Worksheets with answers help apply these concepts practically, making learning relevant and impactful for students.
Overtime Pay Calculation
Piecewise functions are ideal for modeling overtime pay systems. For example, employees earn regular pay up to 40 hours and time-and-a-half for hours exceeding 40. Worksheets with answers demonstrate how to define such functions, ensuring accurate pay calculations and reinforcing understanding of piecewise concepts in practical scenarios.
Cost Functions in Manufacturing
Manufacturing cost functions often use piecewise definitions to differentiate between fixed and variable costs. For example, a factory might incur fixed costs up to a certain production level, then variable costs beyond that. Worksheets with answers help students graph these functions, analyzing how costs change with production volume and optimizing manufacturing budgets effectively.
Temperature Changes Over Time
Piecewise functions model temperature changes during heating or cooling phases. For instance, a substance might change phase at a specific temperature, altering the rate of change. Worksheets with answers help students graph and analyze these transitions, understanding how temperature varies over time in real-world scenarios like climate modeling or material phase changes.
Common Mistakes and Solutions
Common errors include misidentifying intervals, incorrect use of open/closed circles, and neglecting discontinuities. Worksheets with answers highlight these mistakes, offering solutions to improve accuracy in graphing piecewise functions.
Misidentifying Domain Intervals
Misidentifying domain intervals is a common mistake, where students incorrectly assign function rules to the wrong intervals. This often leads to incorrect graphing. Worksheets with answers highlight such errors, providing clear solutions and visual aids to ensure accurate interval identification and correct piecewise function representation.
Incorrect Use of Open/Closed Circles
Incorrectly using open or closed circles is a frequent error when graphing piecewise functions. Open circles indicate excluded endpoints, while closed circles denote inclusion. Mixing these can misrepresent the function’s behavior at interval boundaries. Worksheets with answers provide examples to correct this, ensuring precise graphing and accurate function representation.
Neglecting Points of Discontinuity
Neglecting points of discontinuity is a common mistake when graphing piecewise functions. Discontinuities occur where function pieces meet, and failing to identify or mark them correctly can distort the graph’s accuracy. Worksheets with answers highlight these points, helping students recognize and properly represent removable, jump, or infinite discontinuities in their graphs.

Advanced Tips for Graphing
Advanced tips for graphing piecewise functions include using technology for accuracy, color-coding for clarity, and labeling axes and pieces for better understanding and visualization of the function’s behavior.
Using Technology for Accuracy
Utilizing graphing calculators or software like Desmos simplifies plotting piecewise functions. These tools reduce errors in identifying intervals, open/closed circles, and discontinuities. They also provide precise visualizations, enhancing understanding. Worksheets with answers further verify accuracy, ensuring correct graphing techniques and improving problem-solving skills effectively.
Color-Coding for Clarity
Color-coding is a powerful tool for graphing piecewise functions, helping differentiate between various pieces of the function. Using distinct colors for each interval makes it easier to identify open/closed circles and endpoints. This method enhances readability, ensuring clear visual separation and accurate interpretation of the function’s behavior across its domain.
Labeling Axes and Pieces
Clear labeling of axes and function pieces is crucial for understanding piecewise functions. Labels should include function names, domain intervals, and corresponding y-values. Properly annotated graphs ensure that each piece is easily identifiable, aiding in accurate analysis and preventing confusion when interpreting the function’s behavior across different intervals.
Practice Exercises
Engage with worksheets featuring varied difficulty levels, from graphing basics to complex piecewise functions. Exercises include matching functions to graphs, creating original problems, and interpreting real-world applications.
Worksheets with Varied Difficulty
Worksheets range from basic to advanced, covering graphing, interpreting tables, and real-world applications. Exercises include sketching functions, identifying discontinuities, and calculating values. Advanced sheets focus on creating original piecewise functions and matching graphs to equations, ensuring comprehensive skill development for all learners.
Matching Functions to Graphs
Matching functions to graphs enhances visual understanding and analytical skills. Students identify corresponding pieces, ensuring each function aligns with its graphical representation. This exercise reinforces domain recognition and the use of open or closed circles, bridging algebraic and visual interpretations effectively for deeper comprehension of piecewise functions.
Creating Own Problems
Creating own problems fosters creativity and deepens understanding of piecewise functions. Students design functions, graph them, and craft real-world scenarios, encouraging critical thinking. This hands-on approach prepares them for complex applications, making learning engaging and relevant, while developing problem-solving skills through personalized challenges and innovative thinking in mathematics.
Mastering piecewise functions enhances problem-solving skills and prepares for real-world applications. Continuous practice with worksheets ensures confidence and accuracy in graphing and interpreting these functions effectively.
Piecewise functions involve defining different rules for specific domain intervals. Key concepts include identifying intervals, using open/closed circles for endpoints, and plotting discontinuities. Practice with worksheets helps master graphing techniques, interpret tables of values, and apply functions to real-world scenarios like cost calculations and overtime pay.
Encouragement for Further Practice
Consistent practice with piecewise functions is key to mastery. Utilize worksheets and online tools to refine graphing skills and explore real-world applications. Video tutorials and interactive exercises can deepen understanding and build confidence in handling discontinuities and interval-based functions effectively.

Additional Resources
Recommended worksheets, online graphing tools, and video tutorials provide comprehensive support for mastering piecewise functions, offering interactive learning and detailed explanations.
Recommended Worksheets
Find comprehensive graphing piecewise functions worksheets with answers online. These worksheets offer detailed answer keys, step-by-step solutions, and exercises of varied difficulty. Many are free, printable, and suitable for algebra and precalculus students. They include labeled graphs, domain-range identification, and real-world application problems, making them ideal for practice and mastery.
Online Tools for Graphing
Use online tools like Desmos and GeoGebra to graph piecewise functions. These tools offer interactive interfaces for plotting multiple function pieces and visualizing discontinuities. They allow adjustment of intervals and endpoints, making them great for education. Many offer real-time feedback and can be accessed for free to improve your graphing abilities effectively.
Video Tutorials
Video tutorials on platforms like Khan Academy, Coursera, and YouTube offer step-by-step guidance for graphing piecewise functions. These tutorials often include visual explanations, practical examples, and real-world applications. They complement worksheets by providing verbal and visual instruction, helping learners grasp complex concepts and apply them effectively in their studies or professional tasks.